CSP-S 第二轮复习

搜索技术

DFS

LOJ#6043. 「雅礼集训 2017 Day7」蛐蛐国的修墙方案

这道题有一个很有意思的结论： $p[i]$ 是一个排列的时候，所有的点 $i$ 向 $p[i]$ 连边之后会形成若干个环，不会有环 + 链的形状出现。这个是显然的，如果出现环 + 链就会出现 $p[i]=p[j]$ ，而 $p$ 是一个排列，显然矛盾。

由于题目要求每一个点的度数均为 $1$ ，那么对于每一个偶环，确定一条边的状态就可以确定其他的所有边。这样我们就可以很简单的做这道题目了，但是时间复杂度为 $\Theta(2^{\frac{n}{2}})$ , 不可以接受。

考虑优化，对于点数小于 $4$ （必定点数等于 $2$ ）的环，我们可以直接决定出来哪条边是左括号，哪条边是右括号，这样就可以做到， $\Theta(2^{\frac{n}{4}})$ , 可以承受。这个剪枝是非常强力的。


#include <bits/stdc++.h>
using namespace std;

int N, P[110], num, Belong[110], Color[110], Size[110], Vis[110];
int Cnt[2];

bool Check() {
    Cnt[0] = Cnt[1] = 0;
    for (int i = 1; i <= N; i++) {
        Cnt[Vis[Belong[i]] ^ Color[i]]++;
        if (Cnt[0] > Cnt[1]) return false;
    }
    if (Cnt[0] != Cnt[1]) return false;
    return true;
}

void Dfs(int now) {
    if (now > num) {
        if (Check()) {
            for (int i = 1; i <= N; i++) {
                cout << (Vis[Belong[i]] ^ Color[i] ? '(' : ')');
            }
            exit(0);
        }
        return;
    }
    Vis[now] = true;
    Dfs(now + 1);
    if (Size[now] > 1) {
        Vis[now] = false;
        Dfs(now + 1);
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> N;
    for (int i = 1; i <= N; i++) {
        cin >> P[i];
    }

    for (int i = 1; i <= N; i++) {
        if (Belong[i] == 0) {
            Belong[i] = ++num;
            bool flag = false;
            for (int j = P[i]; j != i; j = P[j]) {
                flag ^= 1;
                Color[j] = flag;
                Belong[j] = num;
                Size[num]++;
            }
        }
    }



    Dfs(1);
    return 0;
}

BFS

「APIO2015」雅加达的摩天楼

LOJ 传送

设状态 $(i,j)$ 表示，当前在第 $i$ 个点，当前的 doge 跳跃能力为 $j$ 。

当 $j \le \sqrt n$ 的时候，只有 $\Theta(n \sqrt n)$ 个状态；

当 $j > \sqrt n$ 的时候，只有 $\Theta(m \sqrt n)$ 个状态；

$(i,j)$ 可以转移到 $(i - j, j)$ 和 $(i + j, j)$ 两个地方，爆搜即可。

记得使用 std::bitset 判重。

时间复杂度： $\Theta((n+m)\sqrt n)$

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 3e4 + 10;

int N, M;
queue<tuple<int, int, int> > Q;
vector<int> Doge[MAXN];
bitset<MAXN> Hash[MAXN];
bitset<MAXN> Vis;
int S, T;

void Insert(int i, int j, int step) {
	if (!Vis[i]) {
		Vis[i] = true;
		for (int x : Doge[i]) {
			if (!Hash[i].test(x)) {
				Hash[i].set(x);
				Q.emplace(i, x, step);
			}
		}
	}
	if (!Hash[i].test(j)) {
		Hash[i].set(j);
		Q.emplace(i, j, step);
	}
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	
	cin >> N >> M;
	for (int i = 0, b, p; i < M; i++) {
		cin >> b >> p;
		if (i == 0) S = b;
		else if (i == 1) T = b;
		Doge[b].push_back(p);
	}
	if (S == T) {
		cout << 0 << endl;
		return 0;
	}

	Vis[S] = true;
	for (int x : Doge[S]) {
		if (!Hash[S].test(x)) {
			Hash[S].set(x);
			Q.emplace(S, x, 0);
		}
	}

	while(Q.size()) {
		static int i, j, step;
		tie(i, j, step) = Q.front();
		Q.pop();
		if (i - j == T || i + j == T) {
			cout << step + 1 << endl;
			return 0;
		}
		if (i - j >= 0) {
			Insert(i - j, j, step + 1);
		}
		if (i + j < N) {
			Insert(i + j, j, step + 1);
		}
	}
	
	cout << -1 << endl;
	return 0;
}

图论

最短路

「HNOI2014」道路堵塞

LOJ 传送

首先有一个结论：删除边后的最短路一定是在最短路上跑一段，然后跳出最短路，然后再跑一段。换言之，就是不在最短路上跑的路径一定是一段连续的路径，不会存在两段及以上（如果两段相等，假设选择原最短路上的路径）。

证明：

这个结论是我猜出来的，现在给出简要证明。

记 $\operatorname{dis}(i)$ 表示路径 $i$ 的长度, $\operatorname{dis}(i,j)$ 表示边 $i \to j$ 的长度。

一条路径表示为 $i=a\to b \to \cdots \to z$

给定一张图：

这张图中我们假设 $i=1 \to 4 \to 5\to 8$ 是最短路，当 $1 \to 4$ 断开时，我们选定了 $j=1 \to 2 \to 3 \to 4 \to 5 \to6 \to 7 \to 8$ 为最短路，如图：

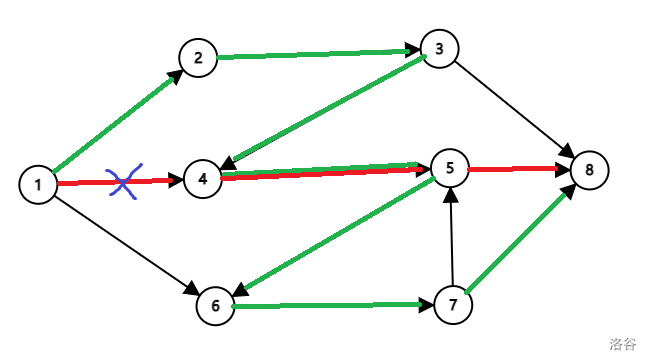
（图中原最短路由红色标出，现在的最短路由绿色标出）

设 $k = 1 \to 2 \to 3 \to 4 \to 5 \to 8$

由于绿色是断开后的最短路，由最短路定义有：

\operatorname{dis}(j) \le \operatorname{dis}(k)

则有

\operatorname{dis}(5,6) + \operatorname{dis}(6,7)+\operatorname{dis}(7,8) \le \operatorname{dis}(5,8)

那么在原图中

1 \to 4 \to 5 \to 6 \to 7 \to 8

才是最短路（如果两段相等，假设选择原最短路上的路径），产生矛盾。

证毕。

接下来讲实现。

我们先以 $1$ 为起点 $n$ 为终点跑一遍 SPFA，并且此时不走给定最短路上的边。然后开始枚举最短路上的点，把它丢进队列，跑 SPFA（dist 数组可以不清空）。

然后每次走到给定最短路上的点，就把这个当前到它的最短路和它到终点的距离（通过最短路到达）丢进一个堆里。每次输出答案前，如果堆的顶部的点在最短路上的位置在当前枚举的的边前，就弹出。最后输出堆顶（如果没有，即为 $-1$ ）。最后把枚举的这条边加进原图，更新这个点出边的 dist。

具体看代码。

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 1e5 + 10;
const int MAXM = 2e5 + 10;

int Head[MAXN];
struct _ {
    int Next, To, Value;
} G[MAXM];
int Cnt = 0;

void Add(int u, int v, int w) {
    G[++Cnt] = {Head[u], v, w};
    Head[u] = Cnt;
}

struct Node {
    int To, Value;
    bool operator<(const Node &o) const {
        return Value > o.Value;
    }
};

int Dist[MAXN];

priority_queue<Node> Heap;

bool Vis[MAXN], Cannot_Use[MAXM];

int Edge[MAXN];

int Id[MAXN], Path_Value[MAXN], Path_Point[MAXN], N, M, L;

void SPFA(int s) {
    queue<int> q;
    q.push(s);
    Vis[s] = true;

    while (q.size()) {
        int u = q.front();
        q.pop();
        Vis[u] = false;
        for (int i = Head[u]; i; i = G[i].Next) {
            if (Cannot_Use[i]) {
                continue;
            }
            int v = G[i].To;
            if (Dist[v] > Dist[u] + G[i].Value) {
                Dist[v] = Dist[u] + G[i].Value;
                if (Id[v]) {
                    Heap.push({Id[v], Dist[v] + Path_Value[Id[v]]});
                } else if (!Vis[v]) {
                    Vis[v] = true;
                    q.push(v);
                }
            }
        }
    }
}

int main() {
    memset(Dist, 0x3f, sizeof Dist);

    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> N >> M >> L;
    for (int i = 1, u, v, w; i <= M; i++) {
        cin >> u >> v >> w;
        Add(u, v, w);
    }

    for (int i = 1; i <= L; i++) {
        cin >> Edge[i];
        Path_Point[i + 1] = G[Edge[i]].To;
        Cannot_Use[Edge[i]] = true;
        Id[Path_Point[i + 1]] = i + 1;
    }

    for (int i = L; i >= 1; i--) {
        Path_Value[i] = Path_Value[i + 1] + G[Edge[i]].Value;
    }

    Dist[1] = 0;
    Id[1] = 1;
    Path_Point[1] = 1;

    SPFA(1);

    for (int i = 1; i <= L; i++) {
        while (Heap.size() && Heap.top().To <= i) {
            Heap.pop();
        }
        if (Heap.size()) {
            cout << Heap.top().Value << endl;
        } else {
            cout << -1 << endl;
        }

        Dist[Path_Point[i + 1]] = Dist[Path_Point[i]] + G[Edge[i]].Value;

        SPFA(Path_Point[i + 1]);
    }
    return 0;
}

最小生成树

树上倍增

首先，我们要使用 Kruskal 或 Prim 求出原图 $G=<V,E>$ 的最小生成树 $G'=<V',E'>$ 。然后我们考虑枚举 $E - E'$ 中的每一条边。将它加入最小生成树中显然会得到一个环。设这条边是 $(u,v)$ 。我们钦定这条边在次小生成树上。这里有一个显然的命题，最小生成树和次小生成树的差距为一条边，利用反证法显然可证。那么答案为最小生成树路径 $root \to u$ 和 $root \to v$ 的最大值再加上这条边的权值，依次枚举每一条非树边取最小值即可。

时间复杂度： $\Theta(m \log m + m \log n)$

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 1e5 + 10;
const int MAXM = 3e5 + 10;

typedef long long ll;

const ll INF = 0x7f7f7f7f7f7f7f7f;

ll N, M;

struct _edge {
    ll u, v, w;
    bool In_MST;

    bool operator<(const _edge &b) const {
        return w < b.w;
    }
} Edge[MAXM];

vector<pair<ll, ll> > G[MAXN];

ll F[MAXN][20], Max[MAXN][20], Max2[MAXN][20], Depth[MAXN];
ll Fa[MAXN];

ll MST, t;

ll Find(int x) {
    return Fa[x] == x ? x : Fa[x] = Find(Fa[x]);
}

void Kuruskal() {
    sort(Edge + 1, Edge + 1 + M);
    int ToT = 0;
    for (int i = 1; i <= M; i++) {
        ll u = Edge[i].u;
        ll v = Edge[i].v;

        ll fu = Find(u);
        ll fv = Find(v);
        if (fu != fv) {
            Fa[fu] = fv;
            ToT++;
            MST += Edge[i].w;
            Edge[i].In_MST = true;
            G[u].push_back({v, Edge[i].w});
            G[v].push_back({u, Edge[i].w});
        }

        if (ToT == N - 1) break;
    }
}

void BFS() {
    queue<int> q;
    q.push(1);
    Depth[1] = 1;
    while (q.size()) {
        auto x = q.front();
        q.pop();
        for (auto i : G[x]) {
            if (Depth[i.first]) continue;
            Depth[i.first] = Depth[x] + 1;
            q.push(i.first);
            F[i.first][0] = x;
            Max[i.first][0] = i.second;
            Max2[i.first][0] = -INF;
            for (int j = 1; j <= 18; j++) {
                F[i.first][j] = F[F[i.first][j - 1]][j - 1];
                Max[i.first][j] = max(Max[i.first][j - 1], Max[F[i.first][j - 1]][j - 1]);
                if (Max[i.first][j - 1] == Max[F[i.first][j - 1]][j - 1]) {
                    Max2[i.first][j] = max(Max2[i.first][j - 1], Max2[F[i.first][j - 1]][j - 1]);
                } else if (Max[i.first][j - 1] < Max[F[i.first][j - 1]][j - 1]) {
                    Max2[i.first][j] = max(Max[i.first][j - 1], Max2[F[i.first][j - 1]][j - 1]);
                } else if (Max[i.first][j - 1] > Max[F[i.first][j - 1]][j - 1]) {
                    Max2[i.first][j] = max(Max2[i.first][j - 1], Max[F[i.first][j - 1]][j - 1]);
                }
            }
        }
    }
}

ll LCA(int x, int y) {
    if (Depth[x] < Depth[y]) swap(x, y);
    for (int i = 18; i >= 0; i--) {
        if (Depth[F[x][i]] >= Depth[y]) {
            x = F[x][i];
        }
    }
    if (x == y) return x;
    for (int i = 18; i >= 0; i--) {
        if (F[x][i] != F[y][i]) {
            x = F[x][i];
            y = F[y][i];
        }
    }
    return F[x][0];
}

ll GetMax(ll x, ll lca, ll val) {
    ll Ans = 0;
    for (int i = 18; i >= 0; i--) {
        if (Depth[F[x][i]] >= Depth[lca]) {
            if (Max[x][i] == val)
                Ans = max(Ans, Max2[x][i]);
            else
                Ans = max(Ans, Max[x][i]);
            x = F[x][i];
        }
    }
    return Ans;
}

void Work() {
    ll Ans = INF;
    for (int i = 1; i <= M; i++) {
        if (Edge[i].In_MST) continue;

        int x = Edge[i].u;
        int y = Edge[i].v;
        ll z = Edge[i].w;
        ll Lca = LCA(x, y);
        ll LMax = GetMax(x, Lca, z);
        ll RMax = GetMax(y, Lca, z);
        if (max(LMax, RMax) != z) {
            Ans = min(Ans, MST + z - max(LMax, RMax));
        }
    }
    cout << Ans << endl;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    
    cin >> N >> M;
    for (int i = 1; i <= N; i++) Fa[i] = i;
    for (int i = 1; i <= M; i++) {
        ll x, y, z;
        cin >> x >> y >> z;
        if (x == y) continue;
        Edge[i] = {x, y, z, false};
    }
    Kuruskal();
    BFS();
    Work();
    return 0;
}

树链剖分

「LNOI2014」LCA

LOJ 传送

题目要求

\sum_{i=l}^r \operatorname{dep}[\operatorname{LCA}(i,z)]

其中 $l,r,z$ 是给定的。

这个式子乍一看没法做，不好化简，那我们将式子的内容放到树上看看表示什么。

假设我们现在枚举到节点 $i(l \le i \le r)$ ，那么可以将 $1 \to i$ 的路径染成蓝色，再将 $1 \to z$ 的路径染成红色，那么被染色两次的点就是 $\operatorname{dep}[\operatorname{LCA}(i,z)]$ 。

但是这样做很慢，瓶颈在于清空和反复做的几个东西，要考虑将做过的东西用起来，设 $f(x,z) = \sum\limits_{i=1}^x \operatorname{dep}[\operatorname{LCA}(i,z)]$ ，那么原式子就可以差分为 $f(r,z) - f(l-1,z)$ 。考虑将询问以差分的形式离线，按照 $f$ 函数的第一个参数进行排序，那么做过的路径就可以用起来了。然后树上加，点权求和可以通过树剖实现，具体实现看代码。

时间复杂度： $\Theta((N+M)\log^2 n)$

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 5e4 + 10;
const int MOD = 201314;

int N, M;
vector<int> G[MAXN];

int Dfn[MAXN], Depth[MAXN], Son[MAXN], Fa[MAXN], Size[MAXN], Top[MAXN], Id[MAXN], Cnt;

void Dfs1(int u) {
    Size[u] = 1;
    for (int v : G[u]) {
        if (v == Fa[u]) continue;
        Depth[v] = Depth[u] + 1;
        Fa[v] = u;
        Dfs1(v);
        Size[u] += Size[v];
        if (Size[v] > Size[Son[u]]) Son[u] = v;
    }
}

void Dfs2(int u, int e) {
    Id[u] = ++Cnt;
    Top[u] = e;
    if (Son[u] != 0) Dfs2(Son[u], e);
    for (int v : G[u]) {
        if (v == Fa[u] || v == Son[u]) continue;
        Dfs2(v, v);
    }
}

struct SegmentTree {
    int LeftTree, RightTree;
    int Value, Tag;
} Tree[MAXN * 4];

void Build(int p, int l, int r) {
    Tree[p].LeftTree = l;
    Tree[p].RightTree = r;
    if (l == r) return;
    int mid = l + r >> 1;
    Build(p * 2, l, mid);
    Build(p * 2 + 1, mid + 1, r);
    Tree[p].Value = (Tree[p * 2].Value + Tree[p * 2 + 1].Value) % MOD;
}

void PushDown(int p) {
    if (Tree[p].Tag) {
        Tree[p * 2].Tag += Tree[p].Tag;
        Tree[p * 2].Tag %= MOD;
        Tree[p * 2 + 1].Tag += Tree[p].Tag;
        Tree[p * 2 + 1].Tag %= MOD;
        Tree[p * 2].Value += (Tree[p * 2].RightTree - Tree[p * 2].LeftTree + 1) * Tree[p].Tag;
        Tree[p * 2].Value %= MOD;
        Tree[p * 2 + 1].Value += (Tree[p * 2 + 1].RightTree - Tree[p * 2 + 1].LeftTree + 1) * Tree[p].Tag;
        Tree[p * 2 + 1].Value %= MOD;
        Tree[p].Tag = 0;
    }
}

int Query(int p, int l, int r) {
    if (l <= Tree[p].LeftTree && Tree[p].RightTree <= r) {
        return Tree[p].Value % MOD;
    }
    PushDown(p);
    int res = 0, Mid = Tree[p].LeftTree + Tree[p].RightTree >> 1;
    if (l <= Mid) res = (res + Query(p * 2, l, r)) % MOD;
    if (r > Mid) res = (res + Query(p * 2 + 1, l, r)) % MOD;
    return res;
}

void UpDate(int p, int l, int r, int d) {
    if (l <= Tree[p].LeftTree && Tree[p].RightTree <= r) {
        Tree[p].Value += (Tree[p].RightTree - Tree[p].LeftTree + 1) * d;
        Tree[p].Tag += d;
        Tree[p].Value %= MOD;
        return;
    }
    PushDown(p);
    int Mid = Tree[p].LeftTree + Tree[p].RightTree >> 1;
    if (l <= Mid) UpDate(p * 2, l, r, d);
    if (r > Mid) UpDate(p * 2 + 1, l, r, d);
    Tree[p].Value = (Tree[p * 2].Value + Tree[p * 2 + 1].Value) % MOD;
}

int QueryRange(int x, int y) {
    int Ans = 0;
    while (Top[x] != Top[y]) {
        if (Depth[Top[x]] < Depth[Top[y]]) swap(x, y);
        Ans = (Ans + Query(1, Id[Top[x]], Id[x])) % MOD;
        x = Fa[Top[x]];
    }
    if (Depth[x] > Depth[y]) swap(x, y);
    Ans += Query(1, Id[x], Id[y]);
    Ans %= MOD;
    return Ans;
}

void UpDateRange(int x, int y, int d = 1) {
    d %= MOD;
    while (Top[x] != Top[y]) {
        if (Depth[Top[x]] < Depth[Top[y]]) swap(x, y);
        UpDate(1, Id[Top[x]], Id[x], d);
        x = Fa[Top[x]];
    }
    if (Depth[x] > Depth[y]) swap(x, y);
    UpDate(1, Id[x], Id[y], d);
}

struct Ask {
    int i, x, id, op;
} Question[MAXN * 2];
int ToT;

int Ans[MAXN];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> N >> M;
    for (int i = 2, x; i <= N; i++) {
        cin >> x;
        x++;
        G[x].push_back(i);
        G[i].push_back(x);
    }

    Dfs1(1);
    Dfs2(1, 1);
    Build(1, 1, N);

    for (int i = 1; i <= M; i++) {
        static int l, r, z;
        cin >> l >> r >> z;
        r++;
        z++;
        Question[++ToT] = {l, z, i, -1};
        Question[++ToT] = {r, z, i, 1};
    }

    sort(Question + 1, Question + 1 + ToT, [](Ask a, Ask b) {
        return a.i < b.i;
    });

    for (int i = 1; i <= ToT; i++) {
        for (int j = Question[i - 1].i + 1; j <= Question[i].i; j++) UpDateRange(1, j);
        Ans[Question[i].id] += Question[i].op * QueryRange(1, Question[i].x);
        Ans[Question[i].id] = (Ans[Question[i].id] + MOD) % MOD;
    }
    for (int i = 1; i <= M; i++) cout << Ans[i] % MOD << endl;
    return 0;
}

树的直径

「APIO2010」巡逻

有一个显然的结论，不加边时每条边都需要走 $2$ 次，答案为 $2(n-1)$ 。

先考虑 $k = 1$ 时怎么做，加了一条边以后会与原来的树构成一个环，显然除了环上的边现在只需要走 $1$ 次，环外的边还是要走 $2$ 次。那就可以得到此时最大收益肯定是连接原树的直径的两端（设直径长度为 $x$ ），此时答案为 $2(n-1)-(x-1)$ 。

再考虑 $k = 2$ 时怎么做。我们此时再加边还会跟原树构成一个环，这个环上的每一条边都只需要走 $1$ 次。但是，如果这个环和我们第一次加边所构成的环重叠，重叠部分都需要走 $2$ 次。所以，我们可以将第一次找出来的直径上每条边边权设为 $-1$ ，再找出直径（设直径长度为 $y$ ），此时答案为 $2(n-1)-(x-1)-(y-1)$ 。

这里有一个问题，为什么第一次选直径一定是最优的？可以参见这里的证明。

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 100010;

int Head[MAXN], Cnt = 1;
struct _ {
    int To, Next, Value;
} G[MAXN << 1];

void _add(int u, int v, int w = 1) {
    G[++Cnt] = {v, Head[u], w};
    Head[u] = Cnt;
}

void Add(int u, int v, int w = 1) {
    _add(u, v, w);
    _add(v, u, w);
}


int Dist[MAXN], Pre[MAXN];
pair<int, int> BFS(int x) {
    memset(Dist, 0, sizeof Dist);
    queue<int> q;
    q.push(x);
    Dist[x] = 1;
    pair<int, int> res = {1, x};
    while (q.size()) {
        int u = q.front();
        q.pop();
        for (int i = Head[u]; i; i = G[i].Next) {
            int v = G[i].To;
            if (Dist[v]) continue;
            Dist[v] = Dist[u] + G[i].Value;
            Pre[v] = i;
            q.push(v);
            if (Dist[v] > res.first) {
                res = {Dist[v], v};
            }
        }
    }
    return res;
}

int N, K, P, Q, Len1, Len2;

int Dp[MAXN];
bitset<MAXN> Vis;
void Dynamic_Programming(int x) {
    Vis[x] = true;
    for (int i = Head[x]; i; i = G[i].Next) {
        int y = G[i].To;
        if (Vis[y]) continue;
        Dynamic_Programming(y);
        Len2 = max(Len2, Dp[x] + Dp[y] + G[i].Value);
        Dp[x] = max(Dp[x], Dp[y] + G[i].Value);
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> N >> K;
    for (int i = 1; i < N; i++) {
        static int u, v;
        cin >> u >> v;
        Add(u, v);
    }
    tie(Len1, P) = BFS(1);
    tie(Len1, Q) = BFS(P);
    Len1--;
    if (K == 1) {
        cout << 2 * (N - 1) - (Len1 - 1) << endl;
        return 0;
    }
    while (Q != P) {
        int i = Pre[Q];
        G[i].Value = -1;
        G[i ^ 1].Value = -1;
        Q = G[i ^ 1].To;
    }
    Dynamic_Programming(1);
    cout << 2 * (N - 1) - (Len1 - 1) - (Len2 - 1) << endl;
    return 0;
}

网络流

「JSOI2016」飞机调度

LOJ 传送

这道题目还是挺板的一道网络流，~~可是不知道为什么 LOJ 上的标签是最短路~~。

首先 最少需要多少架飞机 可以转化为 每架飞机尽量用更多的次数。

所以问题转化为一架飞机能够先飞路线 $i$ ，再飞路线 $j$ 的条件。

定义 $G_{i,j}$ 表示机场 $i$ 到机场 $j$ 并且在机场 $j$ 维修完毕的最短路径长度。

然而这个条件是显然的，需要满足从 $X_i$ 起飞到 $Y_i$ 再在 $Y_i$ 修理 $P_{Y_i}$ 的时间最后再走 $Y_i$ 到 $X_j$ 的最短路 的总时间要早于 $D_j$ ，这样两个机场就是可以由一架飞机走的，形式化的就是如下不等式：

D_i + T_{X_i,Y_i} + P_{Y_i} + G_{Y_i, X_j} \le D_j

对于每一个航线我们将其拆分成左航线和右航线，然后我们可以开始建一张二分图。

将所有左航线和源点连接，容量为 $1$ ；
将所有右航线和汇点连接，容量为 $1$ ；
假设一架飞机可以飞路线 $i$ 和路线 $j$ ，那么可以将 $i$ 对应的左航线和 $j$ 对应的右航线连接，容量为 $\infty$ 。

现在我们使用最少的飞机来飞这几条航线就相当于使用最少的路径来覆盖这一张二分图。

结论：答案为 $M-\text{二分图最大匹配} = M - \text{Max Flow}$ 。

简证：

这是一个经典模型：最小路径覆盖。

首先，每选择一条边相当于合并两个路径，那么我们需要尽可能的多选边，选的边数最多为二分图最大匹配。那么如果不合并的话每一个航线都需要自己独立跑，那么答案为 $M$ ，所以现在的答案为 $M-\text{二分图最大匹配} = M - \text{Max Flow}$ 。

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 500010;

struct _ {
    int To, Next, Value;
} G[MAXN << 1];
int Head[MAXN], Cnt = 1;

void _add(int u, int v, int w) {
    G[++Cnt] = {v, Head[u], w};
    Head[u] = Cnt;
}

void Add(int u, int v, int w) {
    _add(u, v, w);
    _add(v, u, 0);
}

int Depth[MAXN], Hash[MAXN], N, M, S, T;

void BFS() {
    memset(Depth, -1, sizeof Depth);
    memset(Hash, 0, sizeof Hash);
    queue<int> q;
    q.push(T);
    Depth[T] = 0;
    Hash[0]++;

    while (q.size()) {
        int u = q.front();
        q.pop();
        for (int i = Head[u]; i; i = G[i].Next) {
            int v = G[i].To;
            if (Depth[v] != -1) continue;
            Depth[v] = Depth[u] + 1;
            Hash[Depth[v]]++;
            q.push(v);
        }
    }
}

int Max_Flow;

int DFS(int u, int flow) {
    if (u == T) {
        Max_Flow += flow;
        return flow;
    }
    int used = 0;
    for (int i = Head[u]; i; i = G[i].Next) {
        int v = G[i].To;
        if (G[i].Value && Depth[v] + 1 == Depth[u]) {
            int Min = DFS(v, min(G[i].Value, flow - used));
            if (Min) {
                G[i].Value -= Min;
                G[i ^ 1].Value += Min;
                used += Min;
            }
            if (used == flow) {
                return used;
            }
        }
    }

    Hash[Depth[u]]--;
    if (Hash[Depth[u]] == 0) Depth[S] = MAXN - 5;
    Depth[u]++;
    Hash[Depth[u]]++;
    return used;
}

int ISAP() {
    Max_Flow = 0;
    BFS();
    while (Depth[S] < MAXN - 5) DFS(S, 0x3f3f3f3f);
    return Max_Flow;
}

int Graph[510][510], X[510], Y[510], D[510], P[510], Cost[510][510];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> N >> M;
    S = M * 2 + 1, T = M * 2 + 2;

    for (int i = 1; i <= N; i++) {
        cin >> P[i];
    }

    for (int i = 1; i <= N; i++) {
        for (int j = 1; j <= N; j++) {
            cin >> Graph[i][j];
            Cost[i][j] = Graph[i][j];
        }
    }

    for (int i = 1; i <= M; i++) {
        cin >> X[i] >> Y[i] >> D[i];
    }

    for (int i = 1; i <= N; i++) {
        for (int j = 1; j <= N; j++) {
            if (i == j) continue;
            Graph[i][j] = Cost[i][j] + P[j];
        }
    }

    for (int k = 1; k <= N; k++) {
        for (int i = 1; i <= N; i++) {
            for (int j = 1; j <= N; j++) {
                Graph[i][j] = min(Graph[i][j], Graph[i][k] + Graph[k][j]);
            }
        }
    }

    for (int i = 1; i <= M; i++) {
        Add(S, i, 1);
    }
    for (int i = 1; i <= M; i++) {
        Add(i + M, T, 1);
    }
    for (int i = 1; i <= M; i++) {
        for (int j = 1; j <= M; j++) {
            if (D[i] + Cost[X[i]][Y[i]] + P[Y[i]] + Graph[Y[i]][X[j]] <= D[j]) {
                Add(i, j + M, 0x3f3f3f3f);
            }
        }
    }

    cout << M - ISAP() << endl;
    return 0;
}

2-SAT 问题

「ARC069D」Flags

洛谷传送门

首先看到最小距离最大，果断二分答案。

然后问题就转化为第 $i$ 个标志可以放置在坐标 $x_i$ 或坐标 $y_i$ 上的最小距离是否可以比 $x$ 大。

这个问题是不是莫名熟悉，有一个变量有两种取值，并且有一定的约束关系（因为距离限制），然后找有没有可行解。于是你就想到了 2-SAT，然后开心的写了一发，TLE 了。

这里有一个问题，像这样连边的时间复杂度 $\Theta(n^2)$ 的，过不了最大的数据点，考虑优化。这时你需要用到一个 trick 叫做线段树优化建图。首先先对所有可能放旗子的点排序，然后你会发现一个点需要连的点是连续的。可以建一棵线段树，因为有父子关系，所有的父亲像儿子连边。为了方便写代码，我们可以强行要求叶子节点的下表为 $1 \sim 2n$ 。接下来就非常类似于区间询问了，直接递归就行了，总时间复杂度 $\Theta(n\log^2 n)$ 。

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 4e4 * 5 + 10;

int Head[MAXN], Next[MAXN << 2], To[MAXN << 2], ToT;
void Add(int u, int v) {
    To[++ToT] = v;
    Next[ToT] = Head[u];
    Head[u] = ToT;
}

int Dfn[MAXN], Low[MAXN];
bool In_Stack[MAXN];
int Stack[MAXN], Top;
int Index, SCC, N;
int Belong[MAXN];

void Tarjan(int u) {
    Stack[++Top] = u;
    In_Stack[u] = true;
    Dfn[u] = Low[u] = ++Index;
    for (int i = Head[u]; i; i = Next[i]) {
        int v = To[i];
        if (!Dfn[v]) {
            Tarjan(v);
            Low[u] = min(Low[u], Low[v]);
        } else if (In_Stack[v]) {
            Low[u] = min(Low[u], Dfn[v]);
        }
    }

    if (Dfn[u] == Low[u]) {
        ++SCC;
        int v;
        do {
            v = Stack[Top--];
            Belong[v] = SCC;
            In_Stack[v] = false;
        } while (v != u);
    }
}

int GetOpposite(int x) {
    if (x <= N)
        return x + N;
    else
        return x - N;
}

pair<int, int> Flags[MAXN << 1];

int SegmentTree[MAXN << 2], Cnt;
void Build(int p, int l, int r) {
    SegmentTree[p] = ++Cnt;
    if (l == r) {
        Add(SegmentTree[p], GetOpposite(Flags[l].second));
        return;
    }
    int mid = l + r >> 1;
    Build(p << 1, l, mid);
    Build(p << 1 | 1, mid + 1, r);
    Add(SegmentTree[p], SegmentTree[p << 1]);
    Add(SegmentTree[p], SegmentTree[p << 1 | 1]);
}

void Link(int p, int L, int R, int l, int r, int x) {
    if (l > r) return;
    int mid = L + R >> 1;
    if (L == l && R == r)
    	Add(x, SegmentTree[p]);
    else if (r <= mid)
        Link(p << 1, L, mid, l, r, x);
    else if (l > mid)
        Link(p << 1 | 1, mid + 1, R, l, r, x);
    else {
        Link(p << 1, L, mid, l, mid, x);
        Link(p << 1 | 1, mid + 1, R, mid + 1, r, x);
    }
}

bool Check(int x) {
    ToT = Top = Index = SCC = 0;
    memset(Head, 0, sizeof Head);
    memset(Dfn, 0, sizeof Dfn);
    memset(Low, 0, sizeof Low);
    memset(In_Stack, 0, sizeof In_Stack);
    Build(1, 1, Cnt = 2 * N);
    for (int i = 1; i <= 2 * N; i++) {
        static int l, r;
        l = upper_bound(Flags + 1, Flags + 1 + 2 * N, make_pair(Flags[i].first - x, 0x3f3f3f3f)) - Flags;
        r = upper_bound(Flags + 1, Flags + 1 + 2 * N, make_pair(Flags[i].first + x - 1, 0x3f3f3f3f)) - Flags - 1;
        Link(1, 1, 2 * N, l, i - 1, Flags[i].second);
        Link(1, 1, 2 * N, i + 1, r, Flags[i].second);
    }
    for (int i = 1;
         i <= 2 * N; i++) {
        if (!Dfn[i]) Tarjan(i);
    }
    for (int i = 1; i <= N; i++) {
        if (Belong[i] == Belong[i + N]) {
            return false;
        }
    }
    return true;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> N;
    for (int i = 1; i <= N; i++) {
        cin >> Flags[i].first >> Flags[i + N].first;
        Flags[i].second = i;
        Flags[i + N].second = i + N;
    }

    sort(Flags + 1, Flags + 1 + 2 * N);

    int l = 0, r = Flags[2 * N].first - Flags[1].first + 1, mid, Ans = -1;

    while (l <= r) {
        mid = l + r >> 1;
        if (Check(mid)) {
            l = mid + 1;
            Ans = mid;
        } else {
            r = mid - 1;
        }
    }

    cout << Ans << endl;
    return 0;
}

费用流

「NOI2012」美食节

LOJ 传送

考虑费用流。

首先费用提前计算，第 $j$ 个厨师倒数第 $k$ 个做第 $i$ 道菜的费用是 $k \times t_{i,j}$ ，因为最后的 $k$ 个人都需要等待这一道菜。

开始建图。

每道菜向源点连一条容量为 $p_i$ 费用为 $0$ 的边；
每个厨师拆成 $n$ 个点，向汇点连一条容量为 $1$ 费用为 $0$ 的点。
第 $i$ 道菜向第 $j$ 个初始所拆出来的第 $k$ 个点连一条容量为 $1$ 费用为 $k \times t_{i,j}$ 的边。

然后跑一次 MCMF。

这样子可以获得 $60$ 分的高分。

这里有一个 trick 叫做动态开点。

由于我们每次跑 SPFA 增广，只能找出一条增广路，所以我们可以暂时不连不需要的边。一开始我们将每个厨师拆成一个点进行连边，在遍历增广路的时候我们对每个厨师添加下一个点，并按照上述第 $3$ 个连边方式连边。

代码

#include <bits/stdc++.h>
using namespace std;

const int MAXN = 1e5 + 10, MAXM = 4e7 + 10;
const int INF = 0x3f3f3f3f;

int N, M;

struct _ {
    int To, Next, Flow, Cost;
} G[MAXN];
int Head[MAXN], Cnt = 1;

void _add(int u, int v, int w, int c) {
    G[++Cnt] = {v, Head[u], w, c};
    Head[u] = Cnt;
}

void Add(int u, int v, int w, int c) {
    _add(u, v, w, c);
    _add(v, u, 0, -c);
}

int Dist[MAXN], Pre[MAXN], Incf[MAXN];
bool Vis[MAXN];
int T, S;

bool SPFA() {
    memset(Dist, 0x3f, sizeof Dist);
    queue<int> q;
    q.push(S);
    Vis[S] = true;
    Dist[S] = 0;
    Incf[S] = INF;
    Incf[T] = 0;
    while (q.size()) {
        int u = q.front();
        q.pop();
        Vis[u] = false;
        for (int i = Head[u]; i; i = G[i].Next) {
            const int &v = G[i].To, &w = G[i].Flow, &c = G[i].Cost;
            if (!w || Dist[v] <= Dist[u] + c) continue;
            Dist[v] = Dist[u] + c;
            Incf[v] = min(w, Incf[u]);
            Pre[v] = i;
            if (!Vis[v]) {
                q.push(v);
                Vis[v] = true;
            }
        }
    }
    return Incf[T];
}

int MaxFlow, MinCost;
int P[MAXN], A[50][150], CYB;

void UpDate() {
    MaxFlow += Incf[T];
    MinCost += Dist[T] * Incf[T];
    int x = T;
    while (x != S) {
        int i = Pre[x];
        G[i].Flow -= Incf[T];
        G[i ^ 1].Flow += Incf[T];
        x = G[i ^ 1].To;
    }
    x = G[Pre[T] ^ 1].To;
    P[++CYB] = P[x];
    Add(CYB, T, 1, 0);
    for (int i = Head[x]; i; i = G[i].Next) {
        int v = G[i].To, w = G[i ^ 1].Cost;
        if (v == T) continue;
        w += A[v][P[x]];
        Add(v, CYB, 1, w);
    }
}

void MCMF() {
    while (SPFA()) UpDate();
}

int main() {
    scanf("%d %d", &N, &M);
    S = 0, T = CYB = N + M + 1;
    for (int i = 1, x; i <= N; i++) {
        scanf("%d", &x);
        Add(S, i, x, 0);
    }
    for (int i = 1; i <= N; i++) {
        for (int j = 1; j <= M; j++) {
            scanf("%d", &A[i][j]);
            Add(i, N + j, 1, A[i][j]);
        }
    }
    for (int i = 1; i <= M; i++) {
        Add(N + i, T, 1, 0);
        P[N + i] = i;
    }
    MCMF();
    cout << MinCost << endl;
}

虚树

「SDOI2011」消耗战

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2.5e5 + 10;
const int MAXM = 5e5 + 10;

int N;

int Head1[MAXN], Head2[MAXN], Cnt1, Cnt2;

struct _ {
    int To, Next;
    long long Value;
} G1[MAXM << 1], G2[MAXM << 1];

void _add(int *head, int &cnt, _ *g, int x, int y, long long v) {
    g[++cnt].Next = head[x];
    g[cnt].To = y;
    g[cnt].Value = v;
    head[x] = cnt;
}

void Add1(int u, int v, long long w) {
    _add(Head1, Cnt1, G1, u, v, w);
    _add(Head1, Cnt1, G1, v, u, w);
}

void Add2(int u, int v, long long w = 0) {
    _add(Head2, Cnt2, G2, u, v, w);
    // _add(Head2, Cnt2, G2, v, u, w);
}

int Dfn[MAXN], Depth[MAXN], Fa[MAXN][30];

int M, H[MAXN], Stack[MAXN], Top, K;

long long Min[MAXN], Dp[MAXN], Index;

void dfs(int u) {
    Dfn[u] = ++Index;
    for (int i = 1; i <= 17; i++) {
        Fa[u][i] = Fa[Fa[u][i - 1]][i - 1];
    }
    for (int i = Head1[u]; i; i = G1[i].Next) {
        int v = G1[i].To;
        if (v != Fa[u][0]) {
            Fa[v][0] = u;
            Depth[v] = Depth[u] + 1;
            Min[v] = min(Min[u], G1[i].Value);
            dfs(v);
        }
    }
}

int LCA(int a, int b) {
    if (Depth[a] < Depth[b]) swap(a, b);
    for (int i = 17; i >= 0; i--) {
        if (Depth[Fa[a][i]] >= Depth[b]) {
            a = Fa[a][i];
        }
    }
    if (a == b) return a;
    for (int i = 17; i >= 0; i--) {
        if (Fa[a][i] != Fa[b][i]) {
            a = Fa[a][i];
            b = Fa[b][i];
        }
    }
    return Fa[a][0];
}

void Dynamic_Programming(int u) {
    if (!Head2[u]) {
        Dp[u] = Min[u];
        return;
    }
    Dp[u] = 0;
    for (int i = Head2[u]; i; i = G2[i].Next) {
        int v = G2[i].To;
        Dynamic_Programming(v);
        Dp[u] += Dp[v];
    }
    Dp[u] = min(Dp[u], Min[u]);
    Head2[u] = 0;
}

void insert(int u) {
    if (Top == 1) {
        if (u != 1) Stack[++Top] = u;
        return;
    } else {
        int l = LCA(u, Stack[Top]);
        if (l == Stack[Top]) return;
        for (; Top > 1 && Dfn[Stack[Top - 1]] >= Dfn[l]; Top--) {
            Add2(Stack[Top - 1], Stack[Top]);
        }
        if (Stack[Top] != l) {
            Add2(l, Stack[Top]);
            Stack[Top] = l;
        }
        Stack[++Top] = u;
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> N;
    for (int i = 1; i < N; i++) {
        int u, v;
        long long w;
        cin >> u >> v >> w;
        Add1(u, v, w);
    }
    Depth[1] = 1;
    Min[1] = 0x7fffffffffffffff;
    dfs(1);
    cin >> M;
    while (M--) {
        cin >> K;
        for (int i = 1; i <= K; i++) {
            cin >> H[i];
        }
        sort(H + 1, H + 1 + K, [](int a, int b) {
            return Dfn[a] < Dfn[b];
        });
        Cnt2 = 0;
        Stack[Top = 1] = 1;
        for (int i = 1, l; i <= K; i++) {
            insert(H[i]);
        }
        for (; Top > 1; Top--) {
            Add2(Stack[Top - 1], Stack[Top]);
        }
        Dynamic_Programming(1);
        cout << Dp[1] << endl;
    }
    return 0;
}

动态规划

线性 DP

「ZJOI2006」超级麻将

定义 $f_{i,j,k,0/1}$ 表示现在点数为 $i$ ，点数为 $i - 1$ 的牌出了 $j$ 张，点数为 $i - 2$ 的牌出了 $k$ 张，是否出过对子的情况下能否打完。

Case1 出对子

$f_{i,j,k,1} = f_{i,j,k,1}\lor f_{i,j,k-1,0}$

Case2 出刻子：

$f_{i,j,k,1} = f_{i,j,k,1}\lor f_{i,j,k-3,1}$
$f_{i,j,k,0} = f_{i,j,k,0}\lor f_{i,j,k-3,0}$

$f_{i,j,k,1} = f_{i,j,k,1}\lor f_{i,j,k-4,1}$
$f_{i,j,k,0} = f_{i,j,k,0}\lor f_{i,j,k-4,0}$

Case3 出顺子

对于 $f_{i,j,k,0}$ 可以考虑出 $k$ 个顺子：
$f_{i,j,k,1} = f_{i,j,k,1}\lor f_{i-1,a_{i-2}-k,j-k,1}$
$f_{i,j,k,0} = f_{i,j,k,0}\lor f_{i-1,a_{i-2}-k,j-k,0}$

#include <bits/stdc++.h>
using namespace std;

int N, A[110];
bool Dp[110][110][110][2];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> N;
    while (N--) {
        memset(Dp, 0, sizeof Dp);
        for (int i = 1; i <= 100; i++) cin >> A[i];
        Dp[0][0][0][0] = true;
        for (int i = 1; i <= 100; i++) {
            for (int j = 0; j <= A[i - 1]; j++) {
                for (int k = 0; k <= A[i]; k++) {
                    if (k > 1) Dp[i][j][k][1] |= Dp[i][j][k - 2][0];
                    if (k > 2) {
                        Dp[i][j][k][1] |= Dp[i][j][k - 3][1];
                        Dp[i][j][k][0] |= Dp[i][j][k - 3][0];
                    }
                    if (k > 3) {
                        Dp[i][j][k][1] |= Dp[i][j][k - 4][1];
                        Dp[i][j][k][0] |= Dp[i][j][k - 4][0];
                    }
                    if (j >= k && A[i - 2] >= k) {
                        Dp[i][j][k][0] |= Dp[i - 1][A[i - 2] - k][j - k][0];
                        Dp[i][j][k][1] |= Dp[i - 1][A[i - 2] - k][j - k][1];
                    }
                }
            }
        }
        cout << Dp[100][A[99]][A[100]][1] << endl;
    }

    return 0;
}

区间 DP

数位 DP

「ZJOI2010」数字计数

树形 DP

状压 DP

「美团 CodeM 初赛 Round B」送外卖2

看到任务比较少，容易想到状态压缩。

分析每个任务的状态，一共有三种，分别为还没有去取，取在手上但是没有送达，已经送达。

考虑使用三进制状压，设 $dp_{i,j}$ 表示当前在第 $i$ 个点，任务的状态为 $j$ 的最小花费。

显然的，从第 $i$ 个点到第 $j$ 个点，肯定走最短路最好，先要使用 Floyd 求出最短路，并记 $dist_{i,j}$ 表示 $i$ 和 $j$ 的最短路。

假设当前状态为 $i$ ，现在位于第 $j$ 个点，枚举到任务 $k$ ：

第 $k$ 个任务的状态为 $0$ （还没有去取），并且 $dp_{j,i}+dist_{j,s_k} \le r_k$ （取完后没有达到任务结束的时间），设 $i'$ 是 $i$ 在三进制下将 $k$ 对应那一位状态加 $1$ 后新的状态，那么 $dp_{s_k,i'} = \min\big\{dp_{s_k,i'},\max\{l_k\,dp_{j,i}+dist_{j,s_k}\}\big\}$ ；
第 $k$ 个任务的状态为 $1$ （取在手上但是没有送达），并且 $dp_{j,i}+dist_{j,t_k} \le r_k$ （送完后没有达到任务结束的时间），设 $i'$ 是 $i$ 在三进制下将 $k$ 对应那一位状态加 $1$ 后新的状态，那么 $dp_{t_k,i'} = \min\big\{dp_{t_k,i'},dp_{j,i}+dist_{j,t_k}\big\}$ ；

时间复杂度为 $\Theta(nq3^q)$

#include <bits/stdc++.h>
using namespace std;

int N, M, Q;
struct qwq {
    int s, t, l, r;
} Task[20];
int Dp[30][59049 + 10], Dist[30][30], Base[20], Ans;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> N >> M >> Q;

    memset(Dist, 0x3f, sizeof Dist);
    for (int i = 1, u, v, w; i <= M; i++) {
        cin >> u >> v >> w;
        Dist[u][v] = min(Dist[u][v], w);
    }
    for (int i = 1; i <= N; i++) Dist[i][i] = 0;

    for (int i = 1; i <= Q; i++) {
        cin >> Task[i].s >> Task[i].t >> Task[i].l >> Task[i].r;
    }

    for (int k = 1; k <= N; k++) {
        for (int i = 1; i <= N; i++) {
            for (int j = 1; j <= N; j++) {
                Dist[i][j] = min(Dist[i][k] + Dist[k][j], Dist[i][j]);
            }
        }
    }

    Base[0] = 1;
    for (int i = 1; i <= Q; i++) Base[i] = Base[i - 1] * 3;

    memset(Dp, 0x3f, sizeof Dp);
    Dp[1][0] = 0;
    for (int i = 0; i <= Base[Q] - 1; i++) {
        for (int j = 1; j <= N; j++) {
            for (int k = 1; k <= Q; k++) {
                int bit = i % Base[k] / Base[k - 1];
                if (bit == 0 && Dp[j][i] + Dist[j][Task[k].s] <= Task[k].r) {
                    Dp[Task[k].s][i + Base[k - 1]] = min(Dp[Task[k].s][i + Base[k - 1]], max(Task[k].l, Dp[j][i] + Dist[j][Task[k].s]));
                }
                if (bit == 1 && Dp[j][i] + Dist[j][Task[k].t] <= Task[k].r) {
                    Dp[Task[k].t][i + Base[k - 1]] = min(Dp[Task[k].t][i + Base[k - 1]], Dp[j][i] + Dist[j][Task[k].t]);
                }
            }
        }
    }

    for (int i = 1; i <= N; i++) {
        for (int j = 0; j <= Base[Q] - 1; j++) {
            if (Dp[i][j] >= 0x3f3f3f3f) continue;
            int CYB = 0;
            for (int k = 1; k <= Q; k++) {
                CYB += ((j % Base[k] / Base[k - 1]) == 2 ? 1 : 0);
            }
            Ans = max(Ans, CYB);
        }
    }

    cout << Ans << endl;
    return 0;
}

概率 DP

「雅礼集训 2018 Day1」树

设 $dp_{i,j}$ 表示由 $i$ 个节点构成且深度为 $j$ 的树的个数。

根据数学期望的定义，答案为 $\frac{1}{(n-1)!}\sum_{i=1}^n (i \times dp_{n,i})$ 。

因为第 $i(i > 1)$ 个节点的父亲是从 $[1,i)$ 的节点里随机出来的，那么 $2$ 号节点的父亲必定就是 $1$ 号节点。于是有两个点的状态是确定下来的。

初值显然有 $dp_{1,1} = dp_{2,2} = 1$ 。

接下来分类讨论，讨论最深的节点在不在 $2$ 的子树中。

dp_{i,j} = \sum_{k=1}^{i-2}\sum_{l=1}^k\begin{pmatrix}i-2\\k-1\end{pmatrix}f_{k,l}+f_{i-k,j}+\sum_{k=1}^{i-1}\sum_{l=1}^j\begin{pmatrix}i-2\\k-1\end{pmatrix}f_{k,j-1}+f_{i-k,l}

时间复杂度为 $\Theta(n^4)$ 。

#include <bits/stdc++.h>
using namespace std;
const int _ = 30;

int n, p, C[_][_];

namespace task1 {
double dp[_][_];

double fac(int x) {
    double res = 1.0;
    for (int i = 1; i <= x; ++i) res = res * i;
    return res;
}

void main() {
    dp[1][1] = dp[2][2] = 1;
    for (int i = 3; i <= n; ++i)
        for (int j = 2; j <= i; ++j) {
            for (int k = 1; k <= i - 2; ++k)
                for (int l = 1; l <= min(j - 2, k); ++l)
                    dp[i][j] += dp[k][l] * dp[i - k][j] * C[i - 2][k - 1];
            for (int k = 1; k <= i - 1; ++k)
                for (int l = 1; l <= j; ++l)
                    dp[i][j] += dp[k][j - 1] * dp[i - k][l] * C[i - 2][k - 1];
        }
    double ans = 0;
    for (int i = 1; i <= n; ++i) ans += i * dp[n][i];
    printf("%d\n", (int)(ans / fac(n - 1) + 0.5));
}
}

namespace task2 {
int dp[_][_];

int fac(int x) {
    int res = 1;
    for (int i = 1; i <= x; ++i) res = 1ll * res * i % p;
    return res;
}

int power(int x, int k) {
    int res = 1;
    for (; k; k >>= 1, x = 1ll * x * x % p)
        if (k & 1) res = 1ll * res * x % p;
    return res % p;
}

void main() {
    dp[1][1] = dp[2][2] = 1;
    for (int i = 3; i <= n; ++i)
        for (int j = 2; j <= i; ++j) {
            for (int k = 1; k <= i - 2; ++k)
                for (int l = 1; l <= min(j - 2, k); ++l)
                    dp[i][j] = (dp[i][j] + 1ll * dp[k][l] * dp[i - k][j] % p * C[i - 2][k - 1] % p) % p;
            for (int k = 1; k <= i - 1; ++k)
                for (int l = 1; l <= j; ++l)
                    dp[i][j] = (dp[i][j] + 1ll * dp[k][j - 1] * dp[i - k][l] % p * C[i - 2][k - 1] % p) % p;
        }
    int ans = 0;
    for (int i = 1; i <= n; ++i)
        ans = (ans + 1ll * i * dp[n][i] % p) % p;
    printf("%lld\n", 1ll * ans * power(fac(n - 1), p - 2) % p);
}
}

int main() {
    scanf("%d %d", &n, &p);
    for (int i = 0; i <= n; ++i) C[i][0] = 1;
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= i; ++j)
            C[i][j] = C[i - 1][j] + C[i - 1][j - 1];
    task1 ::main();
    task2 ::main();
    return 0;
}

DP 优化

单调队列优化

「SCOI2010」股票交易

定义 $f_{i,j}$ 表示前 $i$ 天，第 $i$ 天结束的股票数量为 $j$ 的最小花费。

从 $0$ 开始购买： $f_{i,j}=-j* AP_i$
不进行购买： $f_{i,j}=\min\{f_{i-1,j}\}$
买入股票： $f_{i,j}=\max\{f_{i−W−1,k}−(k-j) \times AP_i\}$
卖出股票： $f_{i,j}=\max\{f_{i−W−1,k}+(j-k) \times BP_i\}$

然后第 $3$ 个和第 $4$ 个方程直接上单调队列即可。

#include <bits/stdc++.h>
using namespace std;

int T, MaxP, W;

struct qwq {
    int Ap, Bp, As, Bs;
} Num[2010];

int Dp[2010][2010];
int Queue[2010];
int l, r, Ans;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> T >> MaxP >> W;
    for (int i = 1; i <= T; i++) {
        cin >> Num[i].Ap >> Num[i].Bp >> Num[i].As >> Num[i].Bs;
    }
    memset(Dp, 128, sizeof Dp);
    for (int i = 1; i <= T; i++) {
        for (int j = 0; j <= Num[i].As; j++) {
            Dp[i][j] = -1 * j * Num[i].Ap;
        }
        for (int j = 0; j <= MaxP; j++) {
            Dp[i][j] = max(Dp[i - 1][j], Dp[i][j]);
        }
        if (i <= W) continue;
        l = 1, r = 0;
        for (int j = 0; j <= MaxP; j++) {
            while (l <= r && Queue[l] < j - Num[i].As) l++;
            while (l <= r && Dp[i - W - 1][Queue[r]] + Queue[r] * Num[i].Ap <= Dp[i - W - 1][j] + j * Num[i].Ap) r--;
            Queue[++r] = j;
            if (l <= r) Dp[i][j] = max(Dp[i][j], Dp[i - W - 1][Queue[l]] + Queue[l] * Num[i].Ap - j * Num[i].Ap);
        }
        l = 1, r = 0;
        for (int j = MaxP; j >= 0; j--) {
            while (l <= r && Queue[l] > j + Num[i].Bs) l++;
            while (l <= r && Dp[i - W - 1][Queue[r]] + Queue[r] * Num[i].Bp <= Dp[i - W - 1][j] + j * Num[i].Bp) r--;
            Queue[++r] = j;
            if (l <= r) Dp[i][j] = max(Dp[i][j], Dp[i - W - 1][Queue[l]] + Queue[l] * Num[i].Bp - j * Num[i].Bp);
        }
    }
    for (int i = 0; i <= MaxP; i++) {
        Ans = max(Ans, Dp[T][i]);
    }
    cout << Ans << endl;
    return 0;
}

决策单调性与四边形不等式

斜率优化

高级数据结构优化

「CF1667B」Optimal Partition

洛谷传送门

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 5e5 + 10;
typedef long long ll;

class SegmentTree {
public:
	struct _ {
		int LeftTree, RightTree;
		ll Value;
	} Tree[MAXN << 4];
	void PushUp(int p) {
		Tree[p].Value = max(Tree[p << 1].Value, Tree[p << 1 | 1].Value);
	}
	void Build(int p, int l, int r) {
		Tree[p].LeftTree = l;
		Tree[p].RightTree = r;
		if (l == r) {
			Tree[p].Value = -1e18;
			return;
		}
		int mid = l + r >> 1;
		Build(p << 1, l, mid);
		Build(p << 1 | 1, mid + 1, r);
		PushUp(p);
	}
	ll Query(int p, int l, int r) {
		if (l <= Tree[p].LeftTree && Tree[p].RightTree <= r) {
			return Tree[p].Value;
		}
		int mid = Tree[p].LeftTree + Tree[p].RightTree >> 1;
		ll res = -1e18;
		if (l <= mid) res = max(res, Query(p << 1, l, r));
		if (mid < r) res = max(res, Query(p << 1 | 1, l, r));
		return res;
	}
	void UpDate(int p, int x, ll v) {
		if (Tree[p].LeftTree == Tree[p].RightTree) {
			Tree[p].Value = max(Tree[p].Value, v);
			return;
		}
		int mid = Tree[p].LeftTree + Tree[p].RightTree >> 1;
		if (x <= mid) UpDate(p << 1, x, v);
		else UpDate(p << 1 | 1, x, v);
		return PushUp(p);
	}
} Tree[3];

int N, T;
ll A[MAXN], S[MAXN], s[MAXN], Dp[MAXN];
map<ll, ll> Mp;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin >> T;
	while (T--) {
		cin >> N;
		for (int i = 1; i <= N; i++) {
			cin >> A[i];
			S[i] = s[i] = A[i] + S[i - 1];
		}
		sort(s + 1, s + 1 + N);
		Mp.clear();
		int Index = 0;
		for (int i = 1; i <= N; i++) {
			if (!Mp.count(s[i])) {
				Mp[s[i]] = ++Index;
			}
		}
		for (int i = 1; i <= N; i++) {
			S[i] = Mp[S[i]];
		}
		for (int i = 0; i < 3; i++) {
			Tree[i].Build(1, 1, Index);
			Tree[i].UpDate(1, Mp[0], 0);
		}
		memset(Dp, 0xcf, sizeof Dp);
		for (int i = 1; i <= N; i++) {
			if (S[i] > 1) Dp[i] = max(Dp[i], Tree[2].Query(1, 1, S[i] - 1) + i);
			Dp[i] = max(Dp[i], Tree[1].Query(1, S[i], S[i]));
			if (S[i] < Index) Dp[i] = max(Dp[i], Tree[0].Query(1, S[i] + 1, Index) - i);
			Tree[0].UpDate(1, S[i], Dp[i] + i);
			Tree[1].UpDate(1, S[i], Dp[i]);
			Tree[2].UpDate(1, S[i], Dp[i] - i);
		}
		cout << Dp[N] << endl;
	}
	return 0;
}

数学

这个有时间再复习，反正数学不会就是不会，怎么学都学不会。

高级数据结构

树状数组

遇到都写线段树。

线段树

「ABC133F」Colorful Tree

洛谷传送门

主席树。

建一棵主席树，第 $i$ 个节点的主席树表示的是它到树根的路径中，相同颜色的边条数和长度和的线段树。每一条路径 $u \to v$ 可以转化为 $u \to root + v \to root - 2 \times (\operatorname{LCA}(u,v) \to root)$ 。

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e5 + 10;

int N, Q;
int cnt;
struct SegmentTree {
	int ls, rs;
	int tot, sum;
} Tree[MAXN * 60];

vector<pair<int, pair<int, int> > > G[MAXN]; // To, Color, Len

int Fa[MAXN][20], Depth[MAXN];
int Dist[MAXN];
int Root[MAXN];

int Build(int l, int r) {
	int p = ++cnt;
	Tree[p].sum = Tree[p].tot = 0;
	if (l == r) return p;
	int mid = l + r >> 1;
	Tree[p].ls = Build(l, mid);
	Tree[p].rs = Build(mid+ 1, r);
	return p;
}

int Change(int p, int l, int r, int x, int y) {
	int rt = ++cnt;
	Tree[rt] = Tree[p];
	Tree[rt].tot++;
	Tree[rt].sum += y;
	int mid = l + r >> 1;
	if (l == r) return rt;
	if (x <= mid)
		Tree[rt].ls = Change(Tree[p].ls, l, mid, x, y);
	else
		Tree[rt].rs = Change(Tree[p].rs, mid + 1, r, x, y);
	return rt;
}

int Query(int p, int l, int r, int x, int y) {
	if (l == r)
		return Tree[p].tot * y - Tree[p].sum;
	int mid = l + r >> 1;
	if (x <= mid)
		return Query(Tree[p].ls, l, mid, x, y);
	else
		return Query(Tree[p].rs, mid + 1, r, x, y);
}

void bfs() {
	queue<int> q;
	q.push(1);
	Depth[1] = 1;
	while (q.size()) {
		auto x = q.front();
		q.pop();
		for (auto y : G[x]) {
			if (Depth[y.first]) continue;
			Depth[y.first] = Depth[x] + 1;
			q.push(y.first);
			Fa[y.first][0] = x;
			Dist[y.first] = Dist[x] + y.second.second;
			Root[y.first] = Change(Root[x], 1, 100000, y.second.first, y.second.second); 
			for (int j = 1; j <= 18; j++) 
				Fa[y.first][j] = Fa[Fa[y.first][j- 1]][j - 1];
		}
	}
}

int LCA(int x, int y) {
	if (Depth[x] < Depth[y]) swap(x, y);
	for (int i = 18; i >= 0; i--) {
		if (Depth[Fa[x][i]] >= Depth[y]) {
			x = Fa[x][i];
		}
	}
	if (x == y) return x;
	for (int i = 18; i >= 0; i--) {
		if (Fa[x][i] != Fa[y][i]) {
			x = Fa[x][i];
			y = Fa[y][i];
		}
	}
	return Fa[x][0];
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin >> N >> Q;
	for (int i = 1 ,u ,v, w, c; i < N; i++) {
		cin >> u >> v >> w >> c;
		G[u].push_back(make_pair(v, make_pair(w, c)));
		G[v].push_back(make_pair(u, make_pair(w, c)));
	}
	Root[1] = Build(1, 100000);
	bfs();
	while (Q--) {
		static int x, y, u, v, lca;
		cin >> x >> y >> u >> v;
		lca = LCA(u, v);
		cout << Dist[u] + Dist[v] - 2 * Dist[lca] + Query(Root[u], 1, 100000, x, y) + Query(Root[v], 1, 100000, x, y) - 2 * Query(Root[lca], 1, 100000, x, y) << endl;
	}
	return 0;
}

平衡树

「Ynoi2011」遥远的过去

实在是很久没有做 Ynoi 了。

首先这道题的两个字符串相等定义为他们离散化后的结果相等。

定义字符串 $A$ 的 Rank 数组为 $a$ （ $A/a$ 可以为任意字符）。

因为是动态的，不难想到字符 Hash。

首先字符串 $A$ 是静态的，因为与 Rank 有关，不难想到用平衡树求出所有长度为 $|B|$ 的字串的哈希值。

考虑开一颗值域平衡树来维护字符串 $B$ 的哈希值（Key Value 为 $B_i$ ），但是这里我们需要反过来哈希，即：

\sum_{i = 1} ^ {|B|} b_i \times base^{|B| - i}

然后就做完了。

#include <bits/stdc++.h>
using namespace std;
namespace io {
const int SIZE = (1 << 21) + 1;
char ibuf[SIZE], *iS, *iT, obuf[SIZE], *oS = obuf, *oT = oS + SIZE - 1, c, qu[55];
int f, qr;
// getchar
#define gc() (iS == iT ? (iT = (iS = ibuf) + fread(ibuf, 1, SIZE, stdin), (iS == iT ? EOF : *iS++)) : *iS++)
// print the remaining part
inline void flush() {
    fwrite(obuf, 1, oS - obuf, stdout);
    oS = obuf;
}
// putchar
inline void putc(char x) {
    *oS++ = x;
    if (oS == oT) flush();
}
// input a signed integer
template <class I>
inline void read(I &x) {
    for (f = 1, c = gc(); c < '0' || c > '9'; c = gc())
        if (c == '-') f = -1;
    for (x = 0; c <= '9' && c >= '0'; c = gc()) x = x * 10 + (c & 15);
    x *= f;
}
// print a signed integer
template <class I>
inline void print(I x) {
    if (!x) putc('0');
    if (x < 0) putc('-'), x = -x;
    while (x) qu[++qr] = x % 10 + '0', x /= 10;
    while (qr) putc(qu[qr--]);
}
struct Flusher_ {
    ~Flusher_() {
        flush();
    }
} io_flusher_;
}  // namespace io
using io ::print;
using io ::putc;
using io ::read;

typedef long long ll;
typedef unsigned long long ull;
typedef unsigned int ui;

const ull Hash_Number = 131, MAXN = 2e5 + 10;

ull N, M, Q;
ull A[MAXN], B[MAXN];
ull Power[MAXN];

/*
FHQ Treap
*/

int Size[MAXN], Fa[MAXN], Son[MAXN][2], Rand[MAXN];
int ToT, Value[MAXN], Rank[MAXN], Tag[MAXN], Root;
ull Sum[MAXN], Hash[MAXN];

int MakeNode(int a, int b) {
    ToT++;
    Size[ToT] = 1;
    Son[ToT][0] = Son[ToT][1] = 0;
    Value[ToT] = a;
    Rank[ToT] = b;
    Tag[ToT] = 0;
    Hash[ToT] = Sum[ToT] = Power[b];
    Rand[ToT] = rand();
    return ToT;
}

void PushDown(int p) {
    if (Tag[p]) {
        if (Son[p][0]) {
            Tag[Son[p][0]] += Tag[p];
            Rank[Son[p][0]] += Tag[p];
            Hash[Son[p][0]] = Hash[Son[p][0]] * Power[Tag[p]];
            Sum[Son[p][0]] = Sum[Son[p][0]] * Power[Tag[p]];
        }
        if (Son[p][1]) {
            Tag[Son[p][1]] += Tag[p];
            Rank[Son[p][1]] += Tag[p];
            Hash[Son[p][1]] = Hash[Son[p][1]] * Power[Tag[p]];
            Sum[Son[p][1]] = Sum[Son[p][1]] * Power[Tag[p]];
        }
        Tag[p] = 0;
    }
}

void PushUp(int p) {
    Size[p] = Size[Son[p][0]] + Size[Son[p][1]] + 1;
    Sum[p] = Sum[Son[p][0]] + Sum[Son[p][1]] + Power[Rank[p]];
    Hash[p] = Hash[Son[p][0]] + Hash[Son[p][1]] + (Size[Son[p][0]] + 1) * (Power[Rank[p]] + Sum[Son[p][1]]);
}

void Split(int p, int k, int &x, int &y) {
    if (p == 0)
        return void(x = y = 0);
    else {
        PushDown(p);
        if (Value[p] <= k) {
            x = p;
            Split(Son[p][1], k, Son[p][1], y);
            PushUp(x);
        } else {
            y = p;
            Split(Son[p][0], k, x, Son[p][0]);
            PushUp(y);
        }
    }
}

int Merge(int x, int y) {
    if (!x || !y) return x | y;
    PushDown(x);
    PushDown(y);
    if (Rand[x] < Rand[y]) {
        Son[x][1] = Merge(Son[x][1], y);
        PushUp(x);
        return x;
    } else {
        Son[y][0] = Merge(x, Son[y][0]);
        PushUp(y);
        return y;
    }
}

void Change() {
    PushDown(Root);
    Tag[Root]++;
    Rank[Root]++;
    Sum[Root] = Sum[Root] * Power[1];
    Hash[Root] = Hash[Root] * Power[1];
}

void Delete(int x) {
    int a, b, c, d;
    Split(Root, x, a, b);
    Split(a, x - 1, c, d);
    d = Merge(Son[d][0], Son[d][1]);
    Root = Merge(Merge(c, d), b);
}

void Insert(int a, int b) {
    int x, y;
    Split(Root, a, x, y);
    Root = Merge(Merge(x, MakeNode(a, b)), y);
}

/*
Ending~
*/

unordered_map<ull, int> Hash_Table;

int main() {
    srand(time(0));
    read(N);
    read(M);
    read(Q);
    for (int i = 1; i <= N; i++)
        read(A[i]);
    for (int i = 1; i <= M; i++)
        read(B[i]);
    Power[0] = 1;
    for (int i = 1; i <= N; i++)
        Power[i] = Power[i - 1] * Hash_Number;
    for (int i = 1; i <= M; i++) {
        Insert(A[i], M - i);
    }
    Hash_Table[Hash[Root]]++;
    for (int i = M + 1; i <= N; i++) {
        Delete(A[i - M]);
        Change();
        Insert(A[i], 0);
        Hash_Table[Hash[Root]]++;
    }
    Root = ToT = 0;
    for (int i = 1; i <= M; i++) {
        Insert(B[i], M - i);
    }
    while (Q--) {
        static int x, c;
        read(x);
        read(c);
        Delete(B[x]);
        Insert(B[x] = c, M - x);
        print(Hash_Table[Hash[Root]]);
        putc('\n');
    }
    return 0;
}

「Ynoi2014」人人本着正义之名

细节太多，放弃了。

整体二分

Dynamic Rankings

整体二分板子题。

整体二分的题通常需要满足如下条件：

询问的答案具有可二分性
修改对判定答案的贡献互相独立，修改之间互不影响效果
修改如果对判定答案有贡献，则贡献为一确定的与判定标准无关的值
贡献满足交换律，结合律，具有可加性
题目允许使用离线算法

分治： $(ql,qr)$ 为操作的区间， $(l,r)$ 为答案区间
当 $l=r$ 时，所有询问答案为 $l$ 。
否则，按时间顺序遍历所有操作，并用树状数组维护 $[l,mid]$ 范围内的数有多少个。
对于加点、删点操作，直接修改树状数组；
对于询问操作，当答案 $\le mid$ 时把询问放到子任务 $[l,mid]$ ，否则放到子任务 $[mid+1,r]$ 。
所有操作分配完成后，撤回树状数组的修改操作，向下递归。

时间复杂度： $\Theta(n \log^2 n)$

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN = 1e5 + 10;

int Val(int x) {
	return x < 0 ? -1 : 1;
}

int N, M;
int A[MAXN];
struct _ {
	int x, y, K, id;
} Q[MAXN << 2], Temp[MAXN << 2];

int C[MAXN << 2], ToT, Ans[MAXN << 2];
int lb(int x) {
	return x & -x;
}

void UpDate(int x, int v) {
	while (x <= ToT) {
		C[x] += v;
		x += lb(x);
	}
}

int GetSum(int x) {
	int res = 0;
	while (x) {
		res += C[x];
		x -= lb(x);
	}
	return res;
}

void Solve(int l, int r, int L, int R) {
	if (l > r) return;
	if (L == R) {
		for (int i = l; i <= r; i++) {
			if (Q[i].y >= 1) {
				Ans[Q[i].id] = L;
			}
		}
		return;
	}
	int Mid = L + R >> 1;
	int p1 = l - 1, p2 = r + 1;
	for (int i = l; i <= r; i++) {
		if (Q[i].y == -1) {
			if (abs(Q[i].K) <= Mid) UpDate(Q[i].x, Val(Q[i].K)), Temp[++p1] = Q[i];
			else Temp[--p2] = Q[i];
		} else {
			int CYB = GetSum(Q[i].y) - GetSum(Q[i].x - 1);
			if (Q[i].K <= CYB) Temp[++p1] = Q[i];
			else Q[i].K -= CYB, Temp[--p2] = Q[i];
		}
	}
	for (int i = l; i <= p1; i++) {
		Q[i] = Temp[i];
		if (Q[i].y == -1 && abs(Q[i].K) <= Mid) UpDate(Q[i].x, -Val(Q[i].K));
	}
	for (int i = p2; i <= r; i++) {
		Q[i] = Temp[r + p2 - i];
		if (Q[i].y == -1 && abs(Q[i].K) <= Mid) UpDate(Q[i].x, -Val(Q[i].K));
	}
	Solve(l, p1, L, Mid);
	Solve(p2, r, Mid + 1, R);
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);          
	
	cin >> N >> M;
	for (int i = 1; i <= N; i++) {
		cin >> A[i];
		Q[++ToT] = {i, -1, A[i], ToT};
	}
	for (int i = 1; i <= M; i++) {
		static char op;
		static int x, y, k;
		cin >> op;
		if (op == 'Q') {
			cin >> x >> y >> k;
			Q[++ToT] = {x, y, k, ToT};
		} else {
			cin >> x >> y;
			Q[++ToT] = {x, -1, -A[x], ToT};
			Q[++ToT] = {x, -1, y, ToT};
			A[x] = y;
		}
	}
	memset(Ans, -1, sizeof Ans);
	Solve(1, ToT, 0, 1e9);
	for (int i = 1; i <= ToT; i++) {
		if (Ans[i] != -1) {
			cout << Ans[i] << endl;
		}
	}
	return 0;
}

树套树

分块

线性基

圣剑护符

珂朵莉树

LCT

星球联盟

hydro 传送

很裸的 LCT 维护边双连通分量。

用并查集判环，如果出现环，就在 LCT 上将这些点缩成一个点即可。

~~LCT 的题都是模板题。~~

时间复杂度: $\Theta(P \log^2 n)$

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2e5 + 10;

int N, M, P;

int Fa[MAXN], Son[MAXN][2], Size[MAXN];
bool Reverse[MAXN];

int f1[MAXN], f2[MAXN];

void InIt() {
    for (int i = 1; i <= N; i++) {
        f1[i] = f2[i] = i;
        Size[i] = 1;
    }
    return;
}

int Find1(int x) {
    return f1[x] == x ? x : f1[x] = Find1(f1[x]);
}

int Find2(int x) {
    return f2[x] == x ? x : f2[x] = Find2(f2[x]);
}

bool IsRoot(int x) {
    return Son[Find1(Fa[x])][0] != x && Son[Find1(Fa[x])][1] != x;
}

int Get(int x) {
    return Son[Find1(Fa[x])][1] == x;
}

void Rotate(int x) {
    int y = Find1(Fa[x]), z = Find1(Fa[y]), k = Get(x);
    if (!IsRoot(y)) Son[z][Get(y)] = x;
    Son[y][k] = Son[x][!k];
    Fa[Son[x][!k]] = y;
    Son[x][!k] = y;
    Fa[y] = x;
    Fa[x] = z;
    return;
}

void PushDown(int x) {
    if (Reverse[x]) {
        swap(Son[Son[x][0]][0], Son[Son[x][0]][1]);
        swap(Son[Son[x][1]][0], Son[Son[x][1]][1]);
        Reverse[Son[x][0]] ^= 1;
        Reverse[Son[x][1]] ^= 1;
        Reverse[x] ^= 1;
    }
    return;
}

void UpDate(int x) {
    if (!IsRoot(x)) UpDate(Find1(Fa[x]));
    PushDown(x);
    return;
}

void Splay(int x) {
    UpDate(x);
    for (int fa; fa = Find1(Fa[x]), !IsRoot(x); Rotate(x)) {
        if (!IsRoot(fa)) Rotate(Get(fa) == Get(x) ? fa : x);
    }
    return;
}

int Access(int x) {
    int p = 0;
    for (p = 0; x; p = x, x = Find1(Fa[x])) {
        Splay(x);
        Son[x][1] = p;
    }
    return p;
}

void MakeRoot(int p) {
    Access(p);
    Splay(p);
    Reverse[p] ^= 1;
    swap(Son[p][0], Son[p][1]);
    return;
}

void _link(int x, int y) {
    MakeRoot(x);
    Fa[x] = y;
    f2[Find2(x)] = Find2(y);
    return;
}

void Dfs(int x, int y) {
    if (!x) return;
    f1[x] = y;
    Size[y] += Size[x];
    Dfs(Son[x][0], y);
    Dfs(Son[x][1], y);
    return;
}

int Link(int x, int y) {
    x = Find1(x);
    y = Find1(y);
    if (x == y) {
        return Size[x];
    } else if (Find2(x) != Find2(y)) {
        _link(x, y);
        return -1;
    }
    MakeRoot(x);
    Access(y);
    Splay(y);
    Dfs(Son[y][0], y);
    return Size[y];
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> N >> M >> P;
    InIt();
    for (int i = 1, u, v; i <= M; i++) {
        cin >> u >> v;
        Link(u, v);
    }
    for (int i = 1, u, v, CYB; i <= P; i++) {
        cin >> u >> v;
        CYB = Link(u, v);
        if (CYB == -1)
            cout << "No" << endl;
        else
            cout << CYB << endl;
    }
    return 0;
}

CDQ 分治

莫队

「Ynoi2011」WBLT

其他技巧

贪心

「POI2014」KLO-Bricks

为了防止排到后面一样的砖块太多排不开，所以要贪心的每个位置排当前剩余块数最多的颜色的砖块，如果有多个颜色剩余最多，要优先考虑和末尾颜色相同的来防止倒数第二个和最后一个颜色相同。用堆维护当前位置块数最多的颜色取就好了。

#include <bits/stdc++.h>
using namespace std;

int M, P, Q, N;

struct qwq {
    int X, Y;
};

bool operator<(const qwq &a, const qwq &b) {
    if (a.X != b.X) {
        return a.X < b.X;
    }
    if (a.Y == Q) {
        return false;
    }
    return true;
}

priority_queue<qwq> q;

int Ans[1000010];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> M >> P >> Q;
    for (int i = 1; i <= M; i++) {
        qwq CYB;
        cin >> CYB.X;
        N += CYB.X;
        if (i == P) CYB.X--;
        if (i == Q) CYB.X--;

        if (CYB.X < 0) {
            cout << 0;
            return 0;
        }

        CYB.Y = i;

        q.push(CYB);
    }

    Ans[1] = P;
    Ans[N] = Q;

    for (int i = 2; i < N; i++) {
        qwq CYB = q.top();
        qwq TMZ;
        bool SHW = false;
        q.pop();
        if (CYB.Y == P) {
            TMZ = CYB;
            if (!q.empty()) {
                CYB = q.top();
            } else {
                cout << 0;
                return 0;
            }
            q.pop();
            SHW = true;
        }
        Ans[i] = CYB.Y;
        P = CYB.Y;
        if (CYB.X - 1 > 0) {
            q.push({CYB.X - 1, CYB.Y});
        }
        if (SHW == true) {
            q.push(TMZ);
        }
    }

    for (int i = 2; i <= N; i++) {
        if (Ans[i] == Ans[i - 1]) {
            cout << 0;
            return 0;
        }
    }

    for (int i = 1; i < N; i++) {
        cout << Ans[i] << " ";
    }
    cout << Ans[N];
    return 0;
}

根号分治

双指针

CF1720E Misha and Paintings

分治

没找到什么好玩的题目。

模拟退火

~~也是拿来骗分。~~

「NOIP2021」方差

LOJ 传送

首先我们可以发现，对于数列 $a_{i-1},a_i,a_{i+1}$ ，它的差分数组为 $a_{i-1},a_i - a_{i-1},a_{i+1}-a_i$ ，在 $i$ 处进行操作后原数组变为 $a_{i-1},a_{i-1}+a_{i+1}-a_i,a_{i+1}$ ，它的差分数组为 $a_{i-1},a_{i+1}-a_i,a_i - a_{i-1}$ ，所以这一次操作就可以看作交换相邻两项差分。

为什么这样是对的呢？可以用微扰法简单说明下，假设当前的差分排列是符合先递减后递增的，如果在平均数的右边（左边同理）把两个相邻不等的差分 $d_x$ 和 $d_{x+1}$ 交换一下，显然只会让 $a_x$ 变大，而不会改变其他值。这样 $a_x$ 更偏离了平均数，会导致方差变大。

然后，我们开始模拟退火，随机两项交换差分，计算方差，求出答案。

时间复杂度为 $O(\texttt{玄学})$ 。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

ll N, A[10010];
ll Difference[10010], Ans = LLONG_MAX;

ll Cal() {
    ll res = 0;
    for (int i = 1; i <= N; i++) A[i] = A[i - 1] + Difference[i];
    ll Sum = 0;
    for (int i = 1; i <= N; i++) Sum += A[i];
    for (int i = 1; i <= N; i++) res += (A[i] * N - Sum) * (A[i] * N - Sum);
    return res / N;
}

void SA() {
    double t = 1e3;
    while (t > 1e-6) {
        if ((double)clock() / CLOCKS_PER_SEC >= 0.99) {
            cout << Ans << endl;
            exit(0);
        }
        int x = rand() % (N - 1) + 2, y = rand() % (N - 1) + 2;
        swap(Difference[x], Difference[y]);
        ll CYB = Cal();
        if (CYB <= Ans)
            Ans = CYB;
        else if (exp((double)(Ans - Cal()) / t) * RAND_MAX <= rand())
            swap(Difference[x], Difference[y]);
        t *= 0.97;
    }
}

void GetAns() {
    while (true) {
        SA();
    }
}

int main() {
    srand(time(NULL));
    scanf("%d", &N);
    for (int i = 1; i <= N; i++) {
        cin >> A[i];
        Difference[i] = A[i] - A[i - 1];
    }
    sort(Difference + 2, Difference + N / 2 + 1, [](ll a, ll b) {
        return a > b;
    });
    sort(Difference + N / 2 + 1, Difference + 1 + N);
    GetAns();
    return 0;
}

「ICPC2018 南京区域赛」Country Meow

咕咕咕。