[ABC163F] path pass i

题目描述

给定一棵 $n$ 个点的树，给第 $i$ 个点染上颜色 $c_i$，其中，$c_i$ 为 $[1,n]$ 的一个整数。

现在，对于每一种颜色 $k$，你要求出有多少条简单路径满足路径上至少有一个点的颜色为 $k$。

（$1 \le k \le n \le 2\times 10^5$）

思路

正难则反，考虑所有不包含颜色 $i$ 的路径数量。

如果只求一个，非常简单，删掉所有颜色为 $i$ 的节点，然后树会分为很多很多的联通块。然后设共 $k$ 个联通块，第 $i$ 个联通块的大小为 $s_i$，则答案为：

$$\sum\frac{s_i(s_i+1)}{2}$$

然后这样做时间复杂度为 $\Theta(n^2)$ 的，无法接受。

我们设 $sum_i$ 表示我们在树上已经枚举到的过程中，所有颜色为 $i$ 的子树的总大小（如果有包含，记录最大的）。

对于某一节点的每一个子树，找到每一个颜色相同的，之间相隔的点两两可以形成不包含该颜色的路径，用总方案数减去这些方案数即可。

如图，假设现在在做红色（下面称为颜色 $x$）节点，则答案为 $size_y - k$。

那么 $k$ 怎么算呢？

我们在做 $y$ 之前记一个 $sum_x'$，然后昨晚下面的红色节点后在记一个 $sum_x$，那么 $k = sum_x-sum_x'$。

最后我们要干掉与根相连的边，如图：

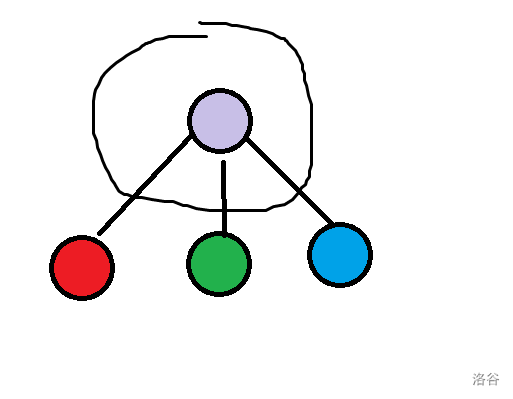
也就是 $n - sum_i$。

具体实现看代码。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN = 2e5 + 10;

ll N;
ll Size[MAXN], Color[MAXN], Ans[MAXN], Count[MAXN];
vector<int> G[MAXN];

ll Sum(ll x) {
	return x * (x + 1) / 2ll;
}

void DFS(int u, int fa) {
	Size[u] = 1;
	ll tmp = Count[Color[u]];
	ll c = Color[u];
	for (int v : G[u]) {
		if (v == fa) continue;
		int t = Count[c];
		DFS(v, u);
		int Ad = Count[c] - t;
		Size[u] += Size[v];
		Ans[c] -= Sum(Size[v] - Ad);
	}
	Count[c] = tmp + Size[u];
	return;
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin >> N;
	for (int i = 1; i <= N; i++) cin >> Color[i];
	for (int i = 1; i < N; i++) {
		static int x, y;
		cin >> x >> y;
		G[x].emplace_back(y);
		G[y].emplace_back(x);
	}
	for (int i = 1; i <= N; i++) Ans[i] = Sum(N);
	DFS(1, -1);
	for (int i = 1; i <= N; i++) {
		cout << Ans[i] - Sum(N - Count[i]) << endl;
	}
	return 0;
}